在財務規劃裡常常會有許多的會計觀念,因此會提到複利的觀念及複利延伸到年金的概念,但理工科的我偏偏完全沒有上過會計,也難怪之前就聽考理財規劃人員專業能力測驗的朋友說,他們準備大概是兩個禮拜,如果是非相關科系起碼要一個月,終於可以深深體會。
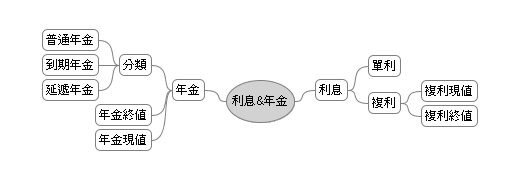
由上面的心智圖可以看到,從利息開始,由計算方式可以分為單利及複利,由於經歷了利息與時間的價值,則延伸出了現值與終值的概念,然後因為複利及某些金流有著固定支出及收入的特性,因此延伸出了年金的觀念,年金依照金流存取的時間點不同又有些不同的分類,在這篇就由利息及終值與現值概念跟大家做介紹。
利息的性質主要決定於本金(principle)、利率(interest rate)、時間(time),而其計算方式分為單利及複利,利息就等於本金X利率X時間。所謂的單利以就是利息的計算只依據本金的大小去做計算,利息在每次記利之後不加入本金繼續於下一期再生利息。同樣的,如果利息加入本金且於下一期的時候與本金一起生利息則稱為複利。
舉例來說,如果有本金1000元,利息為10%,每年計利息1次,到了第三年總共可以拿回多少錢呢?
如果以單利計算,其三年的利息就是1000 X 10% X 3年,等於300元,因此到了第三年可以拿回1300元,而如果以複利計算的話,第一年的利息為1000 X 10%,等於100元,第二年的利息等於(1000 加 第一年的利息)X 10%,等於110元,到了第三年的利息就會等於(1000 加 第一年的利息 加 第二年的利息)X 10%,等於121元,因此第三年拿回本金時,就可以拿到1331元,因此複利就比單利要多出了31元。
而複利會因為複利頻率期數的不同而導致同樣時間下名目利率(nominal rate)與實際上的有效利率(effective yield)不同,舉例來說,如果年利率在12%,但複利的方式改為每季複利一次時(共4次所以每次利率為3%),按照複利的計算方式 1000 X (1 + (3%) )^ 4期就等於1126元,這樣的複利其實若以每年複利一次來計算其利率其實為(1126-1000)/1000 = 12.6%,因此其有效利率的12.6%就較名目上的利率12%還要來的高。所以可以知道只要每年複利的期數超過一次,則有效利率就會大於名目利率。
再以HSBC Direct帳戶來說,照HSBC Direct 往來總約定書條款裡面談到利息的部分說到
新台幣活期存款利息以一年365天計,按滙豐網站針對滙豐 HSBC Direct 活期存款帳戶公告的利率計算,每日單利計息,每月結算付息一次,並於次營業日計入本金。
若現在本金存了10000元在HSBC Direct帳戶,以現在年利率1.5%來說,其日利率就為0.004109%,而以10000元計算則每個月可以得到利息為10000*0.004190%*30等於12.57元,其月利率為0.1257%,則有效年利率就為1.51887%,比起名目利率高出0.01887%多。
接著跟各位介紹複利終值與複利現值的概念,所謂的終值,也就是在存入了一筆本金後,經過了某個固定的複利率及某個期數之後所得到的最終本金與利息總合;而複利現值,照字面來說,也就是"現在的價值",同樣的也是在存入一筆本金之後,經過某個固定的複利率及某個期數之後,得到本利和,再折算回目前的價值。
在會計的觀念裡會提到複利終值因子的概念,其就是將複利本利和變成一個簡單的函式,可能透過查表或者是電腦程式function的方式就可以得到結果,在這邊將複利終值(future value)以FV表示,以n表示期數,以i表示利率,以P表示本金,若要表達某本金P在經過複利某期數之後得到的複利終值則以下列公式表示:

舉例來說假如本金為1000元,每年記利一次,年息10%,則三年後會有多少本利和就用FV=1000*f3,10%=1331元表示。而同樣的既然有複利終值因子就會有複利現值因子,其將複利現值(present value)以PV表示,同樣的以n,i,P表示期數、利率、本金,則下列公式表示。

最後附上這次在南台科技大學的高職教師進修網站的會計事務科上找到的一份文件,這份文件幫助我在理解利息與本金的觀念上有很大的幫助。在下一篇會介紹本金的意義。
1. 貨幣之時間價值
2. 貨幣之時間價值Word檔
3. 會計事務科中級會計學

在〈[金融理財] 理財規劃系列-02 利息的計算〉中有 10 則留言
您好
我想請教
有效年利率的用法
例如
算出 EAR後
能否把 EAR 帶入 普通年金終值 的 i
即 F (n,i) –裡面的i 能否用 EAR帶入
非常感謝你的回答 (方便的話 能否回信到我的信箱[email protected])
hi pong,
不好意思,我不太曉得我有沒有誤解您的意思。
您所說的是先算出EAR之後,
然後在另外的場合中,需要用到"普通年金終值"時,
將EAR帶入F(n,i)的i裡面嗎?
如果是的話,就公式而言,他當然可以,
不過重點在於,您所用的那個狀況下是不是該用普通年金終值的公式。
也許您需要把整個題目完整的講出來,
我才能再幫您做判斷。
我的問題即你所提供的–貨幣的時間價值(PDF檔) 裡面的 {例 14}我的問題如下假如你現在二十歲,有一家人壽保險公司向你招攬保險,條件為你每年繳納$10,000保費,連續繳納二十年,到你四十歲時,可以領回$200,000,以後每五年均領回$200,000,直到你六十五歲,共領取六次,共計$1,200,000,則事實上是保險公司淨賺了$816,837,以下為此例如計算過程與圖示:(假設所有保費的支付與領回的金額均於期末發生)我有問題的部分是在於領回部份
領回部分:
重新計算有效利率(因為乃每五年領回一次):
i=(1+10%)^5-1=0.61051
故每五年領回$200,000,至65歲時其終值為:
200000*F(6,0.61051)=5388741
能否把 F (n,i) –裡面的i 能否用 EAR帶入非常感謝您的回答
hi Pong,
在這個題目的狀況下,
使用EAR帶入是沒有問題的,
主要的原因是因為
保險公司要支出的部分是每五年支出一次,
但,利率卻是每一年複利一次,
也就是五年中複利了5次,
因此有效利率為(1+10%)^5-1=0.61051
也就是,
當利率為61%但每五年才複利一次的結果,
會和利率為10%但每年複利一次的五年後結果一樣。
而同樣的,就保險公司的眼光來看,
每五年固定支出20萬給保戶共支出六次
,也就是年金終值的用法,
所以在這邊FV(n,i)的i,
代入五年複利五次後的有效利率(EAR)是對的。
希望這樣的解釋您可以看懂,
如果沒有懂就在留言吧!!
另外我這邊有用Excel驗算過一次,
如果有需要的話,一樣的可以在留言,
我會留下網址給你下載。
寫在前面
關於HSBC Direct的文章,在墨嗓的不務正業紀實這邊其實已經有許多相關分享與使用心得了,今天會跟大家分享它,是因為我接受了Bloggerads的邀請,所以在這邊要再詳細的介紹它
你好 無意間看到這個資訊 所以我想請教一下
當利率是複利的時候,effective annual rate 會比annual percentage rate 低嗎?
那麼,如果是單利的話,annual percentage rate 是同等 effective annual rate嗎?
請幫幫我~~拜託了!
Novia,
Sorry,現在才回答您!
不過,您的這個問題,在「Effective Annual Rate vs Annual Percentage Rate 實際年利率與平均年利率」這篇文章裡面可以得到答案!給您參考!希望可以幫上您的忙
Hi,Mouson
我想請教根據這篇[金融理財] 理財規劃系列-02 利息的計算
第8段 :
“若現在本金存了10000元在HSBC Direct帳戶,以現在年利率1.5%來說,其日利率就為0.004109%,而以10000元計算則每個月可以得到利息為10000*0.004190%*30等於12.57元,其月利率為0.1257%,則有效年利率就為1.51887%,比起名目利率高出0.01887%多。”
我的疑惑是文中以年利率1.5%來說
日利率為1.5%/365= 0.004109%
每個月可得利息應為10000*0.004109%*30=12.327元,
故月利率為0.12327%,
則有效年利率為0.12327%* 12= 1.47924%
比起名目利率低0.02076%
和您得出的結論有誤差, 請幫解惑, 謝謝!
不好意思現在才看到回應
會有誤差的原因因為
複利計算
而非直接*12的單利計算
Hi, 我的想法與Cedric大類似,
如果以公式來看Re=(1+Rn/m)^m – 1 所以我簡單的代入
Re = (1+1.5%/12)^12 – 1 = 1.51035% → 以月複利看
Re = (1+1.5%/365)^365 – 1 = 1.511% → 以日複利看
若再按照上述的講法,月利率應為10000*(1.5%/365)*30=12.32876即0.1232876%
Re = (1+0.1232876%)^12 – 1 = 1.48952% 反而還比名目利率少?
另外文章的 算式答案有誤 10000*0.004190%*30等於12.57元 這句話是錯的,應為12.327元,這樣算起來實質報酬率似乎小於1.5%了說
謝謝